can stand for, ``The third wise man knows that the second wise
man knows that the first wise man does not know that the first
wise man's spot is white''.
J. McCarthy
jmc@cs.stanford.edu
http://www-formal.stanford.edu/jmc
M. Sato
T. Hayashi
S. Igarashi
Another language for expressing ``knowing that" is given together with axioms and rules of inference and a Kripke type semantics. The formalism is extended to time-dependent knowledge. Completeness and decidability theorems are given. The problem of the wise men with spots on their foreheads and the problem of the unfaithful wives a are expressed in the formalism and solved.
The authors' present addresses are as follows: John McCarthy, Stanford University; Masahiko Sato, University of Tokyo; Takashi Hayashi, Kyushu University; and Shigeru Igarashi, University of Tsukuba.
This research was supported by the Advanced Research Projects Agency of the Department of Defense under ARPA Order No. 2494, Contract MDA9O3.76-C-0206. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of Stanford University, or any agency of the U. S. Government.
The need to represent Information about who knows what in intelligence computer programs was the original motivation for this work. For example, a program that plans trips must know that travel agents know who knows the availability of rooms in hotels. An early problem Is how to represent what people know about other people's knowledge of facts, and even the knowledge of propositions treated In this paper presented some problems that were not treated in previous literature.
We started with the following well known puzzle of the three wise men: A king wishing to know which of his three wise men is the wisest, paints a white spot on each of their foreheads, tells them at least one spot is white, and asks each to determine the color of his spot. After a while the smartest announces that his spot is white reasoning as follows: ``Suppose my spot were black. The second wisest of us would then see a black and a white and would reason that if his spot were black, the dumbest would see two black spots and would conclude that his spot is white on the basis of the king's assurance. He would have announced it by now, so my spot must be white."
In formalizing the puzzle, we don't wish to try to formalize the reasoning about how fast other people reason. Therefore, we will imagine that either the king asks the wise men in sequence whether they know the colors of their spots or that he asks synchronously, ``Do you know the color of your spot" getting a chorus of noes. He asks it again with the same result, but on the third asking, they answer that their spots are white. Needless to say, we are also not formalizing any notion of relative wisdom.
We start with a general set of axioms for knowledge based on
the notation, axioms, and inference
rules of propositional calculus supplemented by the notation
S*p standing for, ``Person S knows
proposition p." Thus
can stand for, ``The third wise man knows that the second wise
man knows that the first wise man does not know that the first
wise man's spot is white''.
We use axiom schemata with subscripted S's as person variables,
subscripted p's and q's as
propositional variables, and a special person constant called
``any fool" and denoted by 0. It is
convenient to Introduce ``any fool" because whatever he knows,
everyone knows that everyone else
knows. ``Any fool" is especially useful when an event occurs
in front of all the knowers, and we
need sentences like, ``
knows that 
knows that 
knows etc.". Here are the schemata:
K0: 
; What a person knows is true.
K1: 
; Any fool knows that what a person knows is true.
K2: 
; What any fool knows,
any fool knows everyone knows, and any fool knows that.
K3: 
;
Any fool knows everyone can do modus ponens.
There are two optional schemata K4 and K5:
K4: 
; Any fool knows that what
someone knows, he knows he knows.
K5: 
;
Any fool knows that what some doesn't know he knows he doesn't know.
If there is only one person S, the system is equivalent to a system of modal logic. Axioms K1-K3 give a system equivalent to what Hughes and Cresswell[1] called T, and K4 and K5 give the modal systems S4 and S5 respectively. We call K4 and K5 the introspective schemata.
It is convenient to write 
as an abbreviation for
; it may be read ``S knows whether p".
On the basis of these schemata we may axiomatize the wise man problem as follows:
C0: 
C1: 
C2: 
C2: 
C3: 
C4: 
C5: 
From K0-K3 and C1-C5 it is possible to prove 
.
C0 is not used in the proof. In some
sense C4 and C5 should not be required. Looking at the
problem sequentially, it should follow
that does not know 
initially, and that even knowing that,
doesn't know 
.
In order to proceed further with the problem, model theoretic semantics is necessary. In what follows, however, we will deal with the puzzle of unfaithful wives (cf. Section 4) rather than that of three wise men, because the latter may be considered as a simplified version of the former. To do so we must extend the system K5 to KT5 in which one can treat the notion of time as well. We will use slightly different notations in the following sections since they are convenient to denote time and have similarity to those used in ordinary modal logics.
We briefly describe the Hilbert-type formulation of the system KT5 in Section 2, and its model theory in Section 3. Finally, we will sketch the outline of the solution to the puzzle of unfaithful wives in this formalism in Section 4. The reader is referred to Sato[2] for details.
The basic language L is a triple 
, where
are denumerable sequence of distinct symbols.
is the set of numerals denoting the corresponding
positive integers. 
will be denoted by 0 and
will be called any fool.
A language L is a triple (Pr, Sp, T), where
Elements in Pr, Sp and T denote propositional variables, persons
and time, respectively. Our arguments henceforth will, unless states
otherwise, always be relative to a language L.
The set of well formed formulas is defined to be the least set Wff such that:
(W1) 
,
(W2) 
,
(W3) 
,
(W4) 
.
The symbols 
and 
denote false and
implication, respectively.
We will make use of the following abbreviations:
For any 
, we define 
inductively
as follows:
(S1) 
(S2) 
(S3) 
We say 
is a subformula of 
if
.
We now define the modal system KT5. The axiom schemata for KT5 are as follows:
(A1) 
(A2) 
(A3) 
(A4) 
(A5) 
(A6) 
,
where 
(A7) 
We have the following two inference rules:
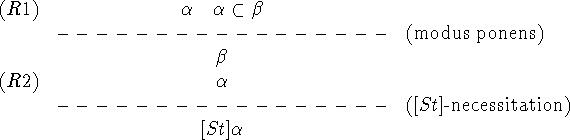
We write 
if there exists a proof of .
For any 
we write 
if 
for some 
.
is said to be consistent if 
.
Let W be any non-empty set (of possible worlds). A model M
on W is a triple
where
and
Given any model M, we define a relation 
as follows:
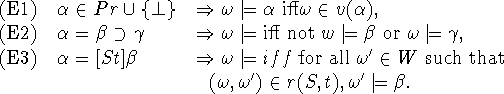
We will write ``
''
if we wish to make M explicit. A formula is
said to be valid in M, denoted by 
, if
for all 
.
(By , we mean 
.) Furthermore,
we will employ the following notation:
A model M is a KT5-model if
(M1) 
(M2) 
for any 
and 
,
(M3) 
for any and 
such that 
,
(M4) r(S,t) is an equivalence relation for any and .
A set of well formed formulas is said to be
realizable if there exists a KT-5 model M
and such that 
.
We now wish to show that each formula provable in KT5 is valid in any KT5-model.
Theorem 1. (Soundness Theorem) If then
for any KT5-model M.
Corollary 2. (Consistency of KT5) is not provable in KT5.
As for the completeness of KT5-models, we have the following theorems.
Theorem 3. (Generalized Completeness Theorem) Any consistent set of well formed formulas is realizable.
Theorem 4. (Completeness and Decidability Theorem) For any ,
is a theorem of KT5 if and only if is valid in all KT5-
models whose cardinality 
, where n is the cardinality
of the finite set 
.
We begin by explaining the notions of knowledge base and knowledge set, which are fundamental for our formalization of the puzzle of unfaithful wives.
Let L be any language. We will make the notion of the totality of one's knowledge explicit by the following definitions:
Definition. 
is a knowledge set for
St if K satisfies the following conditions:
(KS1) K is consistent.
(KS2) 
, where 
.
(KS3) If 
then 
for some 
.
Definition. 
is a knowledge base for
St if B satisfies the following conditions:
(KB1) B is consistent.
(KB2) 
, where 
,
(KB3) If 
then 
for some .
By (KS2) (or (KB2)) we see that any element in
K (or B, esp.) has the form 
.
It is easy to see that if B is a knowledge base for St then
is a knowledge set for St.
Let be consistent. We compare the following three
conditions.
then 
.
then
for some .
then or
.
Then we have the following
Lemma 5. (1), (2) and (3) are equivalent.
We now study the semantical characterization of knowledge sets. Let
be any
KT5-model. For any 
and 
, we define
by:
Since, as we will see below, 
is a knowledge set for St,
we call it the knowledge set for St at w.
Lemma 6. is a knowledge set for St.
Let K be a knowledge set for St. We say 
characterizes K if 
.
Theorem 7. Any knowledge set is characterizable.
The puzzle of unfaithful wives is usually stated as follows:
There was a country in which one million married couples inhabited. Among these one million wives, 40 wives were unfaithful. The situation was that each husband knew whether other men's wives were unfaithful but he did now know whether his wife was unfaithful. One day (call it the first day). the King of the country publicized the following decree:
(i) There is at least one unfaithful wife.
(ii) Each husband knows whether other men's wives are unfaithful or not.
(iii) Every night (from tonight) each man must do his deduction, based on his knowledge so far, and try to prove whether his wife is unfaithful or not.
(iv) Each man, who has succeeded in proving that his wife is unfaithful, must chop off his wife's head next morning.
(v) Every morning each man must see whether somebody chops off his wife's head.
(vi) Each man's knowledge before this decree is publicized consists only of the knowledge about other men's wive's unfaithfulness.
The problem is ``what will happen under this situation?" The answer is that on the 41st day 40 unfaithful wives will have their heads chopped off. We will treat this puzzle in a formal manner.
We will treat this puzzle by assuming that there are
married couples in the country. Then
the language L = (Pr, Sp, T) adequate for this puzzle will be:
where 
denotes ith husband, 
means that
's wife is unfaithful and denotes
ith day.
Let 
denote that k-fold cartesian
product of the vector space 
with addition 
. We define
by 
,
where 
and 
denotes
, resp.). We put 
and
.
We also use 
to denote arbitrary element in 
.
Now, let denote what the King publicized on the first day, and
denote a knowledge base
for 
under the situation 
.
Let us put:
and
where . We also put 
.
Then, as a formalization of the puzzle, we postulate the following
identities:
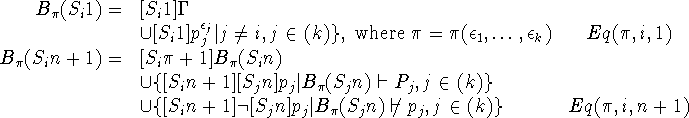
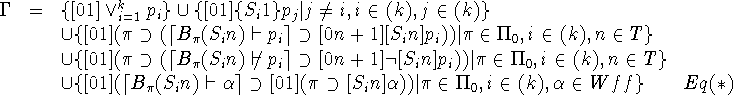
Since the meta-notions such as knowledge base and provability 
cannot be expressed directly in our language, we were forced
to interpret the King's decree into in a somewhat indirect
fashion.
Now, if we read Eq(*) as the definition of , then
we find that the definition is circular, since in order
that may be definable by Eq(*) it is necessary that
are already defined, whereas
are defined in terms of in 
.
So, we will treat these equations as a system 
, 
,
of equations with the unknowns
and .
We will solve 
under the following conditions:
(*) For any 
, 
is consistent.
(**) For any and , is
a knowledge base for .
We think these conditions are natural in view of the intended
meanings of and .
Let us define a norm on
by 
,
where 
.
For any 
and 
, we put
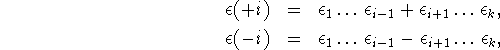
and for any 
, we put
We also put 
.
We define a KT5-model 
as follows:
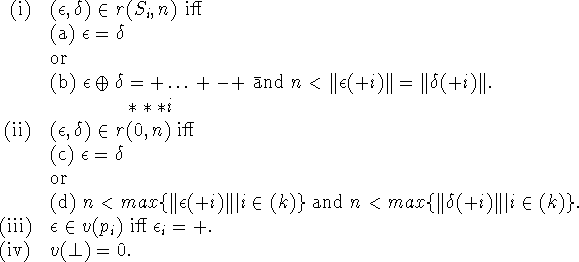
Then we have the following theorem.
Theorem 8. Under the conditions (
) and (
),
has the unique solution
,
where the solution is characterized by the condition:
Thus we have seen that 
may be regarded as the formal
counterpart of the King's decree in our
formal system. The puzzle is then reduced to the
problem of showing that:
We note that we can moreover prove the following:
It is clear that 
and 
follow at once from the condition stated
in theorem 8.